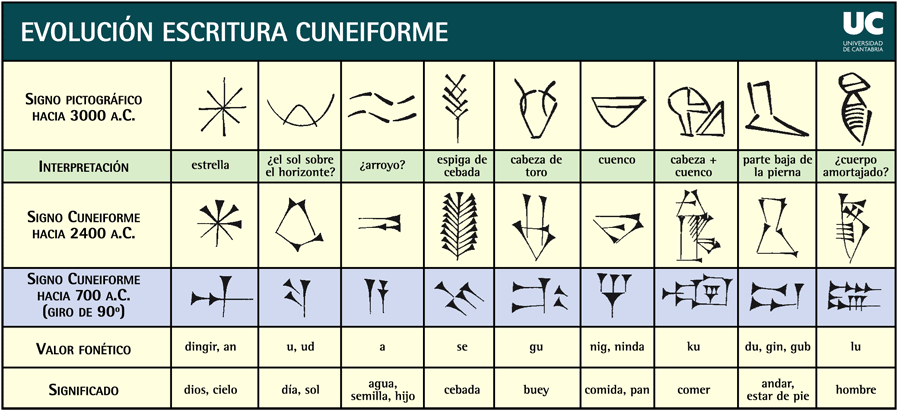
LA EVOLUCION HISTORICA DE LAS MATEMÁTICAS
Las
matemáticas son tan antiguas como como la propia humanidad, existen tejidos,
cerámicas, pinturas y otros diseños prehistóricos en los cuales se puede
evidenciar el interés de los hombres de la época en suplir la necesidad de
contar y utilizar algunas figuras geométricas; se especula que los sistemas de
cálculo primitivos estaban basados en contar con los dedos de las manos por lo
que la base de muchos de sus sistemas numéricos fueran de 5 y 10.
El
sistema de numeración babilónico fue a base de 60 con sus múltiplos y
divisores, evidenciando estos datos en tablillas de arcilla, los babilónicos
lograron con base en este número establecer los calendarios, horas, minutos y
segundos que todavía usamos hoy en día.
Durante
el siglo VI a.C. aproximadamente se inicia una de las épocas doradas en la
matemática gracias a la cultura griega, quienes tomaron como base los avances
de los babilónicos y egipcios para crear las matemáticas abstractas las cuales
se basaban en demostraciones, axiomas y definiciones.
Los
primeros en utilizar esta metodología para el estudio de las matemáticas fueron
Tales de Mileto y Pitágoras de Samos, donde Pitágoras concluyó la importancia
de los números para entender el mundo, sus discípulos realizaron estudios y
aportes a las matemáticas los cuales fueron atribuidos al mismo Pitágoras.
Durante
esta época el estudio de las matemáticas se centró en encontrar métodos
para demostrar las medidas de figuras geométricas, áreas, volúmenes y
longitudes de pirámides, triángulos, cubos, cuadrados, etc.
Como
los griegos utilizaban los números naturales para hacer sus procedimientos se
vieron muy limitados ya que se necesitaba otra clase de números para sus
cálculos, los números irracionales, los cuales fueron descubiertos más tarde
por el matemático Eudoxo basado en el libro de los Elementos creado por
Euclides.
Las
matemáticas griegas llegaron a su auge cuando el matemático Apolonio logró
establecer las ecuaciones de las figuras cónicas, la elipse, parábola,
hipérbola y el círculo quienes fueron usadas más tarde por René Descartes.
Otra
cultura que realizó aportes importantes a las matemáticas fue la cultura India,
quienes a base de sus costumbres comerciales descubrieron que tenían que crear
un nuevo número para representar algunas cantidades y poder resolver
ecuaciones, el número Cero (0) creado por los Hindúes fue el mayor aporte que
realizaron a las matemáticas, con esta inclusión lograron demostrar y
profundizar mucho más en la resolución de ecuaciones lineales y cuadráticas,
además la simbología de los número que utilizamos hoy en día fue creada por la
cultura India.
En
arabia nació uno de los más conocidos matemáticos de la historia Mohammed Ibn
Musa Al-Khwarizmi quien es considerado el padre del álgebra.
La verdad es que fue él quien recopiló los estudios de muchos de los matemáticos más importantes de la historia y lo concentro en un solo legado, con ejemplos, definiciones y métodos de resolución de problemas y ecuaciones.
La verdad es que fue él quien recopiló los estudios de muchos de los matemáticos más importantes de la historia y lo concentro en un solo legado, con ejemplos, definiciones y métodos de resolución de problemas y ecuaciones.
Durante
el renacimiento se realizaron aportes importantes como la creación de una
fórmula para resolver ecuaciones de tercer y cuarto grado por el matemático
italiano Gerolamo Cardano, quien estimuló a otros matemáticos en buscar métodos
para resolver ecuaciones de orden superior como a Évariste Galois y Francois
Viete, cuyos estudios fueron base para los aportes de matemáticos del siglo
siguiente como Pierre Fermat e Isaac Newton.
El
siglo XVII empezó por el descubrimiento de los logaritmos por John Napier
(Neper) y del teorema de Fermat por Pierre Fermat; en este mismo siglo se hizo
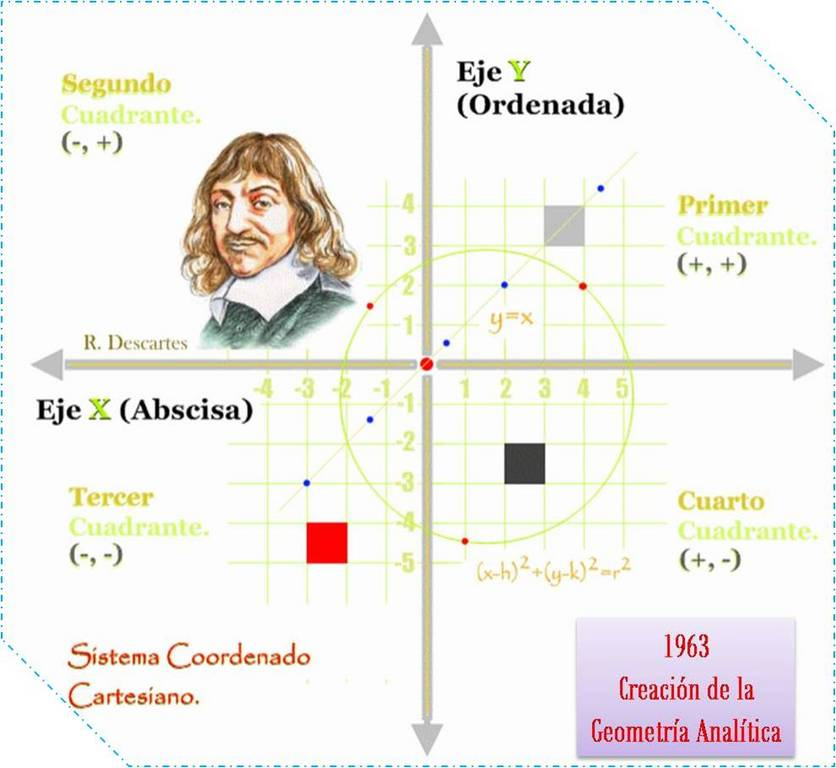
uno de los más importantes aportes por parte de René Descartes quién creo
la geometría analítica combinando la geometría con el álgebra, cuyo
descubrimiento ayudó a Isaac Newton crear los cálculos diferenciales e
integrales.
Otro
descubrimiento que se realizó en este siglo fue la teoría de la probabilidad
por Pascal y Fermat publicado después por Jacques Bernoulli y el concepto de
cálculo descubierto por el alemán Leibniz.
Durante
el siglo XVIII el gran matemático de la época era Leonard Euler quién aportó
grandes conceptos al cálculo y la física.
En
el siglo XIX aparece otro gran matemático, Carl Friedrich Gauss demostró el
concepto de los números complejos, abriendo otra rama de estudio de las
matemáticas; además descubrió la geometría no euclidiana quién fue usada por
Einstein para dar explicaciones a sus investigaciones obre física. También creo
demostraciones, axiomas y ecuaciones, las cuales solo pudieron demostrarse
tiempo después.
Hoy
en día todos estos avances matemáticos hicieron que se creara una maquina tan
inteligente como para también ayudar a resolver problemas matemáticos, la
computadora, ya que con ayuda de ella se han logrado resolver muchas ecuaciones
que dejaron matemáticos anteriores, este avance impulsó algunas ramas de la
matemática y creo otros conceptos mucho más complejos como el estudio de los
algoritmos.
En la actualidad las
matemáticas avanzan de una manera muy rápida, cada día se crean conceptos nuevo
o que complementan uno ya existente, además existen ecuaciones que todavía no
se les ha encontrado solución y también ecuaciones nuevas las cuales también
necesitarán de una demostración.
