EXCEL Y LAS MATEMATICAS

Aqui les dejo uno de los ejemplos que se pueden aprovechar utilizando la tecnologia y la transversalidad con las matematicas: MATEMATICAS Y EXCEL 

https://docs.google.com/spreadsheets/d/1U6vmu3An2og1L3d2oM-TMOnepdgdeeKimrap3JFnqpw/edit?usp=sharing

QUIENES SOMOS

Somos un grupo de estudiantes del programa de licenciatura en matemáticas de la UNAD, quienes en su empeño de formarse profesionalmente en el campo de la pedagogía, han creado este blog como una propuesta de trabajo del curso de historia de las matemáticas, con la visión de que sea una fuente de consulta para docentes y estudiantes, fortaleciendo así conocimientos propios del área de matemáticas.

INTEGRANTES Y EDITORES: 

WILLIAM YARA TIQUE – San Luis de palenque – Casanare  yaratwilliam@gmail.com 
  
CARLOS EDILBERTO RAMIREZ – Bogotá  batsobass@hotmail.com

DANIEL FELIPE SEGURA - Monterrey Casanare,  danyel_16@hotmail.es

MARIA ELISABETH GUERRERO  Duitama  - maelgueca81@gmail.com

PEDRO JOSE RUIZ - Bogotá D.C.

MELISSA ANGELICA SALAS 

LINEA DE TIEMPO Y EVOLUCION DE LAS MATEMATICAS.

Te invitamos a dar un paseo por cada una de las edades y años en que la matemática hizo presencia.
A continuación dale clic en  LINEA DE TIEMPO y navega por nuestra linea de tiempo.

LINEA DE TIEMPO

LA EVOLUCION HISTORICA DE LAS MATEMÁTICAS

LA EVOLUCION HISTORICA DE LAS MATEMÁTICAS

Las matemáticas son tan antiguas como como la propia humanidad, existen tejidos, cerámicas, pinturas y otros diseños prehistóricos en los cuales se puede evidenciar el interés de los hombres de la época en suplir la necesidad de contar y utilizar algunas figuras geométricas; se especula que los sistemas de cálculo primitivos estaban basados en contar con los dedos de las manos por lo que la base de muchos de sus sistemas numéricos fueran de 5 y 10.

Las primeras evidencias matemáticas de matemáticas más avanzadas y organizadas datan del tercer milenio antes de cristo en Babilonia y Egipto las cuales estaban basadas en la aritmética, medias de longitud y figuras geométricas sin saber los conceptos de demostración o axioma.

Los primeros libros egipcios datan de los años 1800 a.C. dan a conocer que el sistema de numeración usado fue a base de 10, logrando hacer operaciones básicas como la suma, la resta, la multiplicación y división; los egipcios fueron los primeros en lograr realizar operaciones con fracciones y crearon métodos aritméticos para calcular el área de figuras geométricas.

El sistema de numeración babilónico fue a base de 60 con sus múltiplos y divisores, evidenciando estos datos en tablillas de arcilla, los babilónicos lograron con base en este número establecer los calendarios, horas, minutos y segundos que todavía usamos hoy en día.

Durante el siglo VI a.C. aproximadamente se inicia una de las épocas doradas en la matemática gracias a la cultura griega, quienes tomaron como base los avances de los babilónicos y egipcios para crear las matemáticas abstractas las cuales se basaban en demostraciones, axiomas y definiciones.

Los primeros en utilizar esta metodología para el estudio de las matemáticas fueron Tales de Mileto y Pitágoras de Samos, donde Pitágoras concluyó la importancia de los números para entender el mundo, sus discípulos realizaron estudios y aportes a las matemáticas los cuales fueron atribuidos al mismo Pitágoras.

Durante esta época el estudio de las matemáticas se  centró en encontrar métodos para demostrar las medidas de figuras geométricas, áreas, volúmenes y longitudes de pirámides, triángulos, cubos, cuadrados, etc.

Como los griegos utilizaban los números naturales para hacer sus procedimientos se vieron muy limitados ya que se necesitaba otra clase de números para sus cálculos, los números irracionales, los cuales fueron descubiertos más tarde por el matemático Eudoxo basado en el libro de los Elementos creado por Euclides.

Las matemáticas griegas llegaron a su auge cuando el matemático Apolonio logró establecer las ecuaciones de las figuras cónicas, la elipse, parábola, hipérbola y el círculo quienes fueron usadas más tarde por René Descartes.

Otra cultura que realizó aportes importantes a las matemáticas fue la cultura India, quienes a base de sus costumbres comerciales descubrieron que tenían que crear un nuevo número para representar algunas cantidades y poder resolver ecuaciones, el número Cero (0) creado por los Hindúes fue el mayor aporte que realizaron a las matemáticas, con esta inclusión lograron demostrar y profundizar mucho más en la resolución de ecuaciones lineales y cuadráticas, además la simbología de los número que utilizamos hoy en día fue creada por la cultura India.

En arabia nació uno de los más conocidos matemáticos de la historia Mohammed Ibn Musa Al-Khwarizmi quien es considerado el padre del álgebra.

La verdad es que fue él quien recopiló los estudios de muchos de los matemáticos más importantes de la historia y lo concentro en un solo legado, con ejemplos, definiciones y métodos de resolución de problemas y ecuaciones.

Durante el renacimiento se realizaron aportes importantes como la creación de una fórmula para resolver ecuaciones de tercer y cuarto grado por el matemático italiano Gerolamo Cardano, quien estimuló a otros matemáticos en buscar métodos para resolver ecuaciones de orden superior como a Évariste Galois y Francois Viete, cuyos estudios fueron base para los aportes de matemáticos del siglo siguiente como Pierre Fermat e Isaac Newton.

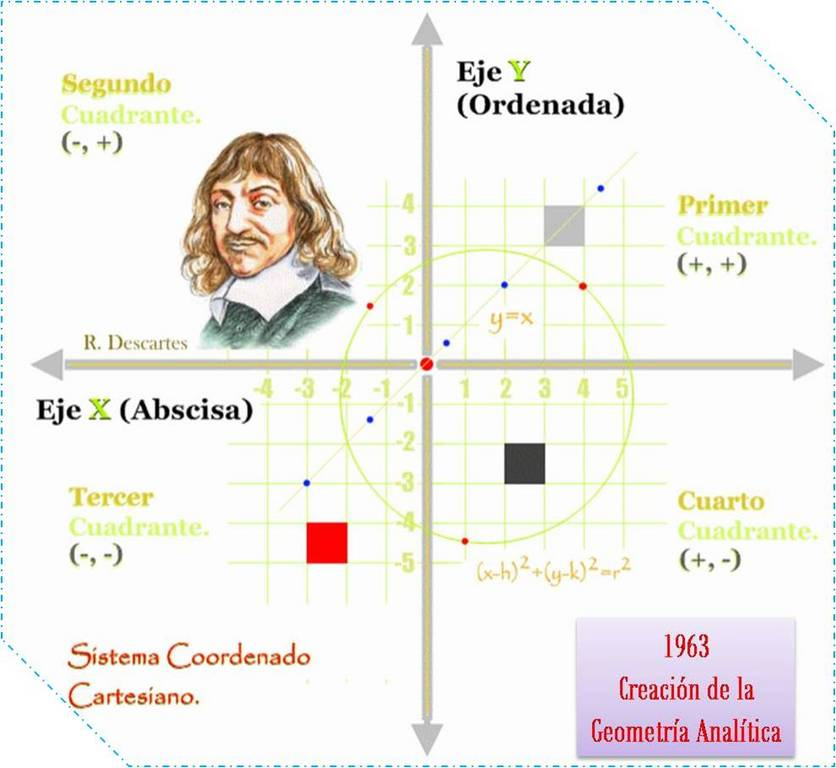
El siglo XVII empezó por el descubrimiento de los logaritmos por John Napier (Neper) y del teorema de Fermat por Pierre Fermat; en este mismo siglo se hizo uno de los más importantes aportes por parte de  René Descartes quién creo la geometría analítica combinando la geometría con el álgebra, cuyo descubrimiento ayudó a Isaac Newton crear los cálculos diferenciales e integrales.

Otro descubrimiento que se realizó en este siglo fue la teoría de la probabilidad por Pascal y Fermat publicado después por Jacques Bernoulli y el concepto de cálculo descubierto por el alemán Leibniz.

Durante el siglo XVIII el gran matemático de la época era Leonard Euler quién aportó grandes conceptos al cálculo y la física.

En el siglo XIX aparece otro gran matemático, Carl Friedrich Gauss demostró el concepto de los números complejos, abriendo otra rama de estudio de las matemáticas; además descubrió la geometría no euclidiana quién fue usada por Einstein para dar explicaciones a sus investigaciones obre física. También creo demostraciones, axiomas y ecuaciones, las cuales solo pudieron demostrarse tiempo después.

Hoy en día todos estos avances matemáticos hicieron que se creara una maquina tan inteligente como para también ayudar a resolver problemas matemáticos, la  computadora, ya que con ayuda de ella se han logrado resolver muchas ecuaciones que dejaron matemáticos anteriores, este avance impulsó algunas ramas de la matemática y creo otros conceptos mucho más complejos como el estudio de los algoritmos.

En la actualidad las matemáticas avanzan de una manera muy rápida, cada día se crean conceptos nuevo o que complementan uno ya existente, además existen ecuaciones que todavía no se les ha encontrado solución y también ecuaciones nuevas las cuales también necesitarán de una demostración.

ENTREVISTA AL EXPERTO

1.      ENTREVISTA AL EXPERTO Y ABSTRACT

a.       ¿Porque considera importante las civilizaciones en la historia de las matemáticas?

-          Porque las civilizaciones han hecho cada una un aporte al desarrollo de las matemáticas. Cuando los primeros humanos  empezaron hacer sus cuentas o llevar sus cuentas ya sean en tablillas de arcilla o en huesos hasta los científicos y los matemáticos modernos que hacen avances en temas aeroespaciales o en desarrollo matemático. Para hacer las cosas que en este momento tenemos al alcance de la mano como por ejemplo los celulares  o la inteligencia artificial posible, entonces es muy importante ver que cada uno de los aportes que han hecho cada una de las culturas a lo largo de la historia han generado ese enriquecimiento y ese desarrollo de las matemáticas, entonces esta la investigación del cálculo, están los desarrollos que han servido para la astronomía y cada una de esos aportes tienen que dárseles importancia como un escalón más en una escalera que realmente no tiene fin escalera infinita en el desarrollo del conocimiento que los hombres tenemos de la matemática. Finalmente como viendo la matemática como representación de la naturaleza porque   es finalmente poder representar todo lo que está en la naturaleza en conceptos matemáticos.

b.      ¿Qué civilización cree que le hizo más aportes a la matemática?

-          Hay muchas civilizaciones que han hecho aportes las más conocidas seria:

La civilización egipcia la cual tenemos evidencia con sus jeroglíficos que dejaron, pero esta la civilización griega con el tema de la trigonometría, está la civilización babilónica o babilonia, está la civilización maya que es poco conocida pero que han hecho aportes con la representación del cero y lo hicieron incluso al parecer unos 600 años antes de la civilización Hindú, obviamente ha hecho muchos desarrollos la principal pienso yo que es la Hindú y también la civilización arábiga que desarrollo el álgebra por ejemplo.

c.       Me podría dar una breve reseña de una de las civilizaciones que más aportes le trajo a la matemática.

-          Bueno pues a mí me gusta mucho la civilización maya porque no es una civilización muy reconocida. Es una civilización que estuvo muy cerca a nosotros digamos que la más cercana que haya tenido un avance matemático evidente pues por eso me parece muy importante reseñarla pues el aporte más importante que ellos tuvieron fue el concepto del cero como un número, como una representación, fue la primera civilización que hizo la primera representación escrita del cero además su sistema de numeración con base 20 y con una base auxiliar cinco que permitió hacer un sistema de multiplicación  muy sencillo en líneas y que permitió que el cruce de esas líneas nos permitieran encontrar los resultados de esa multiplicación, este sistema es más sencillo que el que normalmente se nos enseña en los colegios y pues también para ellos su principal desarrollo matemático no fue para hacer cálculos sino para hacer mediciones astronómicas pues tenemos las principales pienso yo. Los principales motivos que llevo al desarrollo de la matemática uno pues para poder hacer las cuentas de cuanto tengo, de las cosechas, de las ventas, después vino el tema del comercio ese es uno de los temas principales; el segundo tema es la medición de la tierra haciendo mediciones geográficas y el tercero haciendo las mediciones astronómicas; de estos tres  los mayas fueron muy famosos en sus mediciones astronómicas.

-          Crearon unos calendarios muy precisos a pesar de no tener los instrumentos para ver las estrellas para hacer sus mediciones con las matemáticas y pudieron ser muy precisos al hacer un calendario que incluso fue más preciso que el calendario que ahora tenemos que es el gregoriano, eso es básicamente el desarrollo que ellos tuvieron. No vamos a contar su desarrollo en multiplicaciones, divisiones muy grandes o potenciación porque no las necesitaban para lo que ellos querían sin embargo fue un pueblo que tuvo un gran avance comparado con los pueblos que estaban a su alrededor.

INCLUSIÓN DE FORMULAS EN LAS MATEMATICAS, GEOMETRIA, Y CIENCIAS MODERNAS COMO LA TRIGONOMETRIA, CALCULO INTEGRAL Y DIFERENCIAL

INCLUSIÓN DE FORMULAS EN LAS MATEMATICAS, GEOMETRIA, Y CIENCIAS MODERNAS COMO LA TRIGONOMETRIA, CALCULO INTEGRAL Y DIFERENCIAL

Muchas veces la matemática se clasifica en áreas diferentes, la geometría y el álgebra eran dos ramas diferentes de matemáticas hasta que se dedujo que no podían estar separadas y se funcionaron para la creación de nuevos conceptos y una mejor profundización en la matemática moderna.

Las matemáticas griegas se puede notar la combinación del álgebra con la geometría, solo que los autores no veían esta relación, hasta que alrededor de los años 1620 y 1630 un de los más grandes matemáticos de la historia, Pierre Fermat, descubrió y demostró esta relación haciendo estudios sobre un libro perdido de Apolonio y sobre la geometría de curvas, esta relación la demostró por medio de medidas llamadas coordenadas.

Una coordenada es un punto en un plano que satisface unas condiciones geométricas concretas, Fermat las llamaba locus o loci en plural, que significan lugar, un ejemplo muy claro es la definición de la curva de una elipse, “lugar geométrico de todos los puntos del plano tales que la suma de sus distancias a dos puntos dados es la misma”. Esta propiedad de la elipse ya era conocida por los griegos, pero Fermat logró demostrarla algebraicamente tomando esos dos puntos o focos como incógnitas; después Fermat propuso una lista de ecuaciones con focos que representan diferentes curvas en un plano, para resumir, Fermat introdujo los ejes oblicuos en un plano, es decir,  que no se curtan necesariamente por un ángulo, las coordenadas están definidas por dos elementos o números, una perteneciente al eje “x” y la otra al eje “y”, por lo tanto una coordenada se representa como (x,y).

Este nuevo sistema de coordenadas sirvió para que otro gran matemático creara su obra, René Descartes, quién introdujo la teoría de las multidimensiones, sabemos que nuestros ojos ven en tres dimensiones, las dos primeras nos muestran imágenes como si la estuviéramos viendo dibujadas en un plano o en un televisor, pero Descartes pudo definir la tercera dimensión como profundidad, ahora, también dijo que existen muchas más dimensiones, solo que se necesita gran cantidad de imaginación para representarlas.

Además de representar las tres dimensiones de forma geométrica en un plano, también encontró la manera de representar sus coordenadas, ya no se puede usar el mismo sistema de “x” e “y”, sino que se debía ingresar una nueva coordenada la cual llamó “z”, por lo que las coordenadas en una gráfica en tres dimensiones queda (x, y, z); por eso decimos que un plano es bidimensional y el especio es tridimensional, además dijo que una ecuación con tres incógnitas corresponde a una superficie.

Descartes además de introducir la teoría de las multidimensiones, también logro demostrar que las secciones cónicas, antes estudiadas geométricamente, también pudieran expresarse algebraicamente, donde afirma que las secciones cónicas son las líneas más simples después de las rectas,  afirmó que una recta se puede expresar como una ecuación lineal y una sección cónica corresponde a una ecuación cuadrática, después de llegar a este concepto pudo abarcar ecuaciones de orden más alto. En 1643 Fermat al ver la teoría de Descartes con respecto a las secciones cónicas extendió su estudio y las aplicó a tres dimensiones, de lo cual resultaron figuras y ecuaciones como los son los elipsoides, paraboloides y esferas.

Una contribución notable también fue hecha 1691 por el matemático Jakob Bernoulli quien introdujo las coordenadas polares, utilizando un ángulo ϴ y una distancia “r”  para determinar un punto en un plano, ahora las coordenadas son (r,ϴ), que también representan curvas, incluyendo nuevas ecuaciones con nuevas figuras que son difíciles de representar en un plano como por ejemplo la espiral  arquimediana.

SIMBOLOGIA NUMERICA

Simbología Numérica

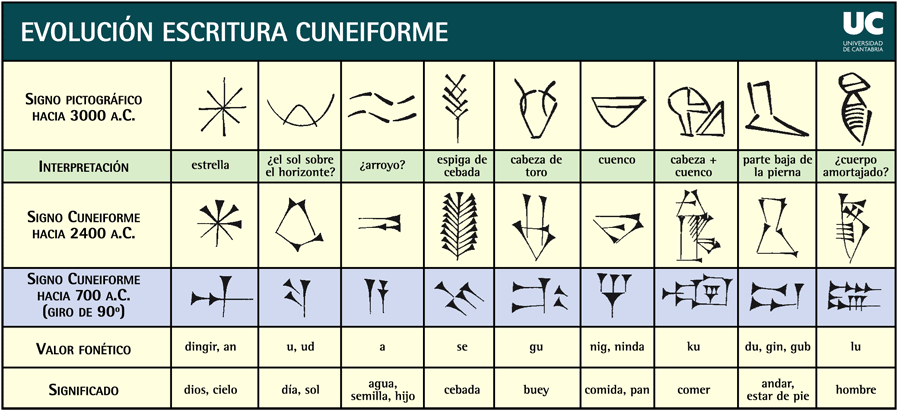
BABILONICA

Este sistema apareció por primera vez alrededor de 1800-1900 a. C. También se acredita como el primer sistema de numeración posicional. Representa los números en la escritura cuneiforme de varios pueblos de Mesopotamia, entre ellos los sumerios, los acadios y los babilonios.

EGIPCIA

Permitía representar números, desde el uno hasta millones, desde el inicio del uso de la escritura jeroglíficos. A principios del tercer milenio a.C. los egipcios disponían del primer sistema desarrollado decima Aunque no era un sistema posicional, permitía el uso de grandes números y también describir pequeñas cantidades en forma de fracciones.

Ojo de Horus

Los egipcios utilizaron un complejo sistema para representar fracciones en medidas agrarias de superficie y volumen, basado en las potencias de 1/2. Los signos de las fracciones mayores fueron tomados de las partes que componían el jeroglífico.